The upside down equation
Turning a curiosity into a maths challenge and a puzzle
28 December 2018
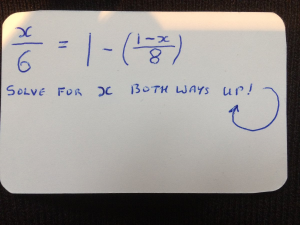
At a recent Christmas gathering, I met Tim Rowett, the child-like toy collector who features on the Grand Illusions channel on YouTube. He was keen to show me his collection of weird and wonderful business cards, but the one that most caught my attention had the above handwritten equation on the back, and the instruction 'Solve for x - both ways up'.
The solution to the equation above involves routine GCSE maths. The curiosity is that if you rotate the card 180 degrees, you get a completely different equation, which can be solved using some slightly harder GCSE maths. It works because the letter x and the numbers 1, 6, 8 and 9 still appear as a letter and numbers when they are turned upside down.
If you want to try to solve both equations, do so now before I reveal the solutions.
* * * * *
The solution to the handwritten equation above is x = 21.
Turned upside, the problem simplifies to x^2 - 9 = 0, and so there are two solutions:
x = 3 or x = -3
The fact that the equation can be turned upside down and still solved turns this otherwise routine maths question into an amusing curiosity.
However it is not completely satisfying. Wouldn't it be better if the equation could be turned upside to give a different equation, while the solution turns out to be unchanged? Or - even better - if the solution to the upside down problem turns out to be the original solution turned upside down? For example, it would be neat if the solution to the first problem was 68, and the solution to the second upside down version was 89.
I set Twitter the challenge of finding an improved version of Tim Rowett's curiosity, and several people took it on. Most successful was Peter Rowlett (note the coincidentally similar surname), who found several nice examples that were closer to the 'perfect' problem. One example was (x+8)/9 = 6/(x+5) which has the solutions 1 and -14 whichever way up you look at it. However, it's not quite perfect for two reasons:
(a) it depends on 5 being written in such a way that it still looks like 5 when you turn it upside down;
(b) the inverted equation and the original turn out to both be equivalent to (x+8)(x+5)=54, whereas in Tim's original version, the two problems to be solved were completely different.
In the correspondence about this maths problem, some people referred to it as a puzzle. I see this more as a curiosity than a puzzle. The only 'puzzling' involved is in solving a quadratic equation, which for anyone confident in maths is a routine task with a well established method of solution.
To be a puzzle, I think there has to be a period when the problem appears to be unsolvable, before the solver has an 'aha' moment.
Here's my suggestion for how to turn the original Tim Rowett curiosity into a puzzle:
"Tim wrote the following equation on a piece of card and asked Adam to work out what x was.
x / 6 = 1 - ((1 - x)/8) [written out in the same format as in the photo at the top of this page]
Adam solved the problem quite quickly and left the card on the table. Beatrice overheard that Adam had solved the problem, walked over and picked up the card. She found the problem harder, but in the end she found two solutions. Curiously, both of Beatrice's solutions were different from Adam's. What were Beatrice's solutions?"
Of course you already know what the twist is, but for somebody who hasn't seen this before, it won't immediately occur to them that the card might be turned upside down. But in the puzzle story, the card had been left on a table, so Beatrice could easily pick it up 'the wrong way up'. The aha moment comes in spotting that you can turn the card upside down, and instead of the other two solutions being a minor flaw, they now become a nice feature of the problem.

